直线的光栅化算法
直线的光栅化算法
write by 九天雁翎(JTianLing) -- www.jtianling.com
看"参考1"碰到的第一个算法,有点意思,总结一下,特别是因为"参考1"没有找到随书的源码下载(Pearson的源码都要教师申请才能下载),自己写点源码,也算是桩乐事。
因为在我们画图的时候,都是以vertex为基础的,所以算法都是以直线(实际是数学中的线段)的起点(x0,y0)加终点(xEnd,yEnd)作为输入来绘制直线的。
基础知识
因为这是第一次提到图形学的算法,这里弄一些预备知识,Glut,OpenGL啥的我倒是不多说了,只是最近我习惯了Mac,所以源代码工程都是XCode的,并且OpenGL包含的目录可能与Win32下不同,这点需要特别注意。
另外,很明显的,OpenGL本身就可以直接绘制直线了。。。。。。所以这里自然不能利用OpenGL的相关功能,不然也没有啥好学的了,更加牵涉不到所谓的"算法",直接看"参考4"即可。
所以,这里只使用一个功能,那就是setPixel函数,此函数也利用OpenGL完成,特别的,为了适应OpenGL ES,我没有如一般的书籍,使用glBegin,glEnd API。
setPixel函数实现如下:
void setPixel(int x, int y) {
GLint vertices[] = {x, y};
glVertexPointer(2, GL_INT, 0, vertices);
glDrawArrays(GL_POINTS, 0, 1);
}
另外,关于绘制直线的环境,这里我为了做到真实显示像素与窗口中坐标点的一一对应,所以如下设置:
static int gw, gh;
void init2d(int w, int h) {
gw = w;
gh = h;
/* attributes */
glClearColor(1.0, 1.0, 1.0, 1.0); /* white background */
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D( - w / 2, w / 2, - h / 2, h / 2);
glMatrixMode(GL_MODELVIEW);
glEnableClientState(GL_VERTEX_ARRAY);
}
并且,还是维持OpenGL原点在中心的特点,同时也方便展示算法在4个象限中的不同。
具体的Glut main函数代码那就非常简单了,这里也贴一下:
int main (int argc, char *argv[]) {
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutInitWindowSize(640, 480);
glutInitWindowPosition(200, 200);
glutCreateWindow("draw lines");
init2d(640, 480);
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
实际我们现在需要关心的也就是display回调函数了。(再次提醒,不明白OpenGL 或者 Glut的,请自行参考本文的"参考4")
利用直线方程
首先,我们知道输入了,
void drawLine(int x0, int y0, int xEnd, int yEnd);
最容易想到的就是直接利用高中学到的直线方程了,这里有2个已知点了,那么直线的点斜式方程就非常容易求出来了。
国外的教科书一般如下:
直线点斜式方程:
(式1)
斜率
截距
将m,b带入式1,对于直线上任意一点,知道x坐标,那么
(式2)
当然,假如更加直观的用直线两点式方程来算y,会更加直接。
通过
直线两点式方程:
(式3)
可以直接求得式2.
可以得出初步的通过直线方程来画直线的算法:
1.计算斜率m
2.从x0开始,每次让x坐标递增1,求得直线的y坐标。
我们可以得到下面的代码:
void drawLineWithEquation(int x0, int y0, int xEnd, int yEnd) {
// slope, notice the difference between the true C/C++ code and the math equation
float m = (float)(yEnd - y0) / (xEnd - x0);
// y = (x - x0) * m + y0;
for (int x = x0; x <= xEnd; ++x) {
int y = lroundf(( x - x0 ) * m + y0);
setPixel(x, y);
}
}
需要特别注意的是,对于强类型语言的变量计算时与数学公式的区别所在,都用整数计算那就会发生严重的精度丢失问题。
我们绘制如下直线:
drawLineWithEquation(0, 0, 300, 50);
drawLineWithEquation(0, 0, 300, 100);
drawLineWithEquation(0, 0, 300, 150);
drawLineWithEquation(0, 0, 300, 300);
drawLineWithEquation(0, 0, 150, 300);
drawLineWithEquation(0, 0, 100, 300);
drawLineWithEquation(0, 0, 50, 300);
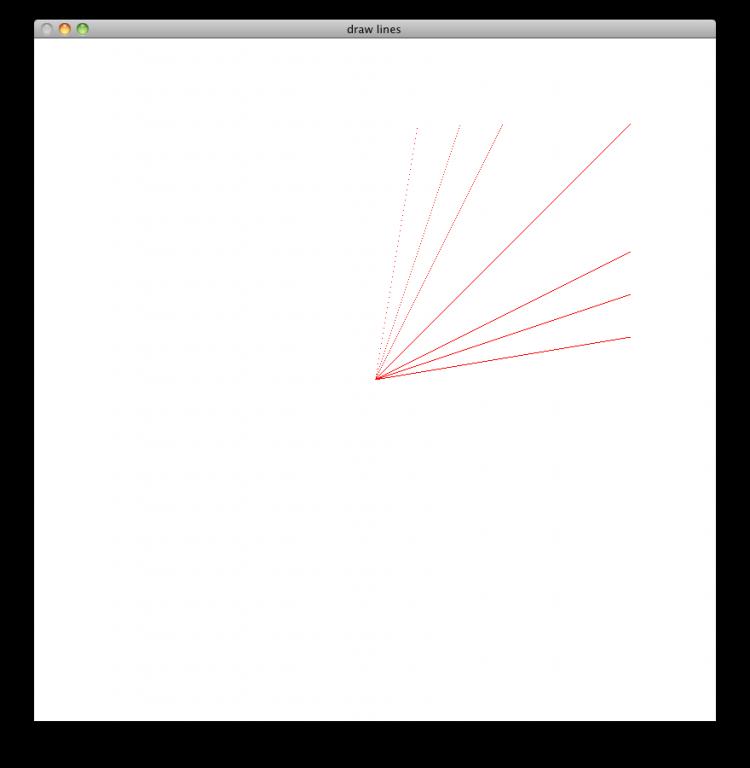
对于一些直线,我们已经可以看到漂亮的结果了。。。。。。。但是,很明显的,当X变化较小,而Y变化较大时,(也就是斜率m>1时)效果非常不好,显示出来的效果可以很明显的看到是一系列离散的点。
原因其实想象就比较容易理解了,因为我们递增的总是X坐标,只需要通过判断斜率,适时的递增Y坐标即可。
那么,就需要根据已知的Y坐标求直线上的点的X坐标了,通过前面的式3,可以直接求得:
(式4)
改进后的代码如下:
void drawLineWithEquation(int x0, int y0, int xEnd, int yEnd) {
// slope, notice the difference between the true C/C++ code and the math equation
float m = (float)(yEnd - y0) / (xEnd - x0);
float mr = 1 / m;
if (m <= 1) {
// when m <= 1: y = (x - x0) * m + y0
for (int x = x0; x <= xEnd; ++x) {
int y = lroundf(( x - x0 ) * m + y0);
setPixel(x, y);
}
}
else {
// when m > 1: x = (y-y0) / m + x0
for (int y = y0; y <= yEnd; ++y) {
int x = lroundf(( y - y0 ) * mr + x0);
setPixel(x, y);
}
}
}
这样效果就好了:

我们一直都用递增来完成直线方程,这里就还是有问题了,因为有可能直线斜率是<0的,(即起点高,终点低),那么我们还需要判断,并通过递减来解决问题。但是实际这样会使得代码进一步复杂化,我们预先通过x0与xEnd,y0与yEnd之间的比较,在的确xEnd,yEnd比x0,y0小的时候,对应的交换xEnd与x0, yEnd与y0即可。从逻辑上来看,因为绘制直线的时候没有方向的概念,那么一条x,y坐标递减的直线总是能看做反方向递增的直线。(相当于反过来画此直线)这样就能在不大量增加代码复杂度的时候确保,总是通过递增能够解决此问题。
但是,假如按上面的判断方式,将有很多种情况,分别是dx,dy与0的比较,以及m与0,1,-1的比较,也就是4*2=8个分支。代码会类似下面这样:
void drawLineWithEquation(int x0, int y0, int xEnd, int yEnd) {
// slope, notice the difference between the true C/C++ code and the math equation
int dx = xEnd - x0;
int dy = yEnd - y0;
float m = (float)dy / dx;
float mr = 1 / m;
if (m <-1) {
if (dy < 0) {
swap(y0, yEnd);
swap(x0, xEnd);
}
for (int y = y0; y <= yEnd; ++y) {
int x = lroundf(( y - y0 ) * mr + x0);
setPixel(x, y);
}
}
else if (m < 0) {
if (dx < 0) {
swap(x0, xEnd);
swap(y0, yEnd);
}
for (int x = x0; x <= xEnd; ++x) {
int y = lroundf(( x - x0 ) * m + y0);
setPixel(x, y);
}
}
else if (m <= 1) {
if (dx < 0) {
swap(x0, xEnd);
swap(y0, yEnd);
}
// when m <= 1: y = (x - x0) * m + y0
for (int x = x0; x <= xEnd; ++x) {
int y = lroundf(( x - x0 ) * m + y0);
setPixel(x, y);
}
}
else {
if (dy < 0) {
swap(y0, yEnd);
swap(x0, xEnd);
}
// when m > 1: x = (y-y0) / m + x0
for (int y = y0; y <= yEnd; ++y) {
int x = lroundf(( y - y0 ) * mr + x0);
setPixel(x, y);
}
}
}
这样又太麻烦了。事实上,问题总是归结与两种情况,一种是X变化大,一种是Y变化大,因此可以仅进行dx,dy的大小判断以减少代码的分支,也就是判断fabs(dx)及fabs(dy)的大小关系。如此,可以得到较为简单的代码:
void drawLineWithEquation(int x0, int y0, int xEnd, int yEnd) {
// slope, notice the difference between the true C/C++ code and the math equation
int dx = xEnd - x0;
int dy = yEnd - y0;
float m = (float)dy / dx;
float mr = 1 / m;
if ( abs(dx) >= abs(dy) ) {
if (dx < 0) {
swap(x0, xEnd);
swap(y0, yEnd);
}
for (int x = x0; x <= xEnd; ++x) {
int y = lroundf( ( x - x0 ) * m + y0);
setPixel(x, y);
}
}
else {
if (dy < 0) {
swap(y0, yEnd);
swap(x0, xEnd);
}
// when m > 1: x = (y-y0) / m + x0
for (int y = y0; y <= yEnd; ++y) {
int x = lroundf(( y - y0 ) * mr + x0);
setPixel(x, y);
}
}
}
作为完整性测试,这里以原点为圆心,生成一个圆,直线的另一个端点总是落在圆周上,以此可以检验4个象限的绘制。
圆的参数方程:
(式5)
然后以15度递增(15度非常有意思,递增时会绘制较为特殊的45,90,180...等较为特殊的角度)以此式完成的测试代码如下:
int r = 300;
for (float theta = PI / 12; theta <= 2 * PI ; theta += PI / 12) {
int x = r * cos(theta);
int y = r * sin(theta);
drawLineWithEquation(0, 0, x, y);
}
最后绘制的效果如下,显示效果基本完美:
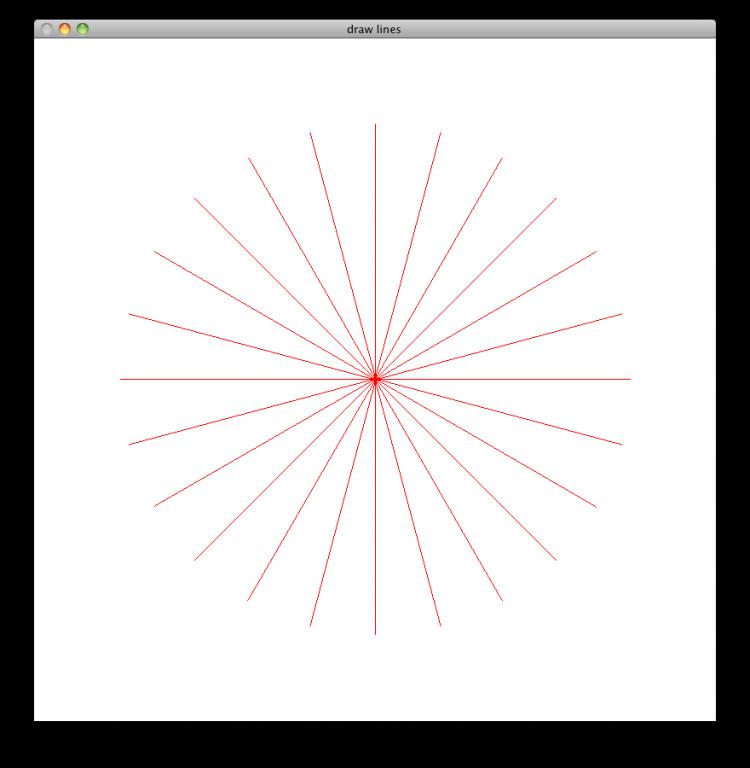
DDA算法(digital differential analyzer)
个人感觉从直线的方程绘制直线的方法想到DDA算法还算比较自然。
观察一下上面通过方程绘制直线的代码,有个地方会觉得明显还可以进一步优化,那就是swap函数的存在。因为在上面的算法种我们总是希望通过递增来解决问题,而事实上,递减又未尝不可,假如可以接受递减,那么就不需要swap的操作了,而同时,又不希望开新的分支来区分递增递减,那么很自然的可以想到,直接将x,y的递增递减量算出来,负的就递减,正的就递增,而我们只需要用+来处理,根本不用关心其符号,因为都正好符合要求。同时,因为x0与xEnd,y0与yEnd的大小判断此时已经不方便作为循环结束的标识(不然又得分支),所以同时提出循环次数,此时循环次数就等于max(fabs(dx),fabs(dy)),就能很自然的得到DDA算法。(这种描述是我自己从代码的优化角度推导出DDA算法的过程,需要更加严格数学推导及描述的,可以参考"参考1“的DDA算法部分。
通过这种思想,可以得出DDA算法的画线代码:
void drawLineWithDDA(int x0, int y0, int xEnd, int yEnd) {
// slope, notice the difference between the true C/C++ code and the math equation
int dx = xEnd - x0;
int dy = yEnd - y0;
float x = x0;
float y = y0;
int steps = max(abs(dx), abs(dy));
float xIncrement = float(dx) / steps;
float yIncrement = float(dy) / steps;
setPixel(x, y);
for (int i = 0; i <= steps; ++i) {
x += xIncrement;
y += yIncrement;
setPixel(lroundf(x), lroundf(y));
}
}
效果不变,这里就不截图了。同时,可以看到,这个算法提炼了一些概念以后,是要比前一个算法效率高的,用每次绘制直线只需要一次的除法替代了循环中的乘法。
简单的说,该算法的效率提升来自从原来直线方程算法的连续计算到离散运算。
但是此算法用到了浮点运算,并且最后有浮点到整数的取整操作,这些操作使得算法效率还有改进的空间。
Bresenham算法
Bresenham算法是由Bresenham 1962年发明,1965年发表,(见WIKI
,"参考3"认为发表的时间就是发明的时间,可能有误)鬼才知道,为啥在那个年代,还在用绘图仪画线时,Bresenham这种牛人是怎么想到这种扭曲,思维跳跃的算法的。突然想到某地方看到一个笑话,话说某个中学生特别讨厌牛顿,莱布尼茨等人。。。。。因为他们不弄出那么一堆奇怪的定理和算法,那么学习会容易的多。。。。呵呵
Bresenham算法是现在硬件和软件光栅化的标准算法。(见"参考2"352面)相比DDA算法的好处在于完全避免了浮点运算,以及DDA算法因为有浮点运算而带来的取整运算,因此更加高效。
不过算法的发明的思维简直是无敌了,pf啊pf......简单的说,该算法简单的说,将DDA的严谨的离散运算都简化成上一个点,下一个点的逻辑判断了。。。。牛啊
该算法书中描述得很多,"参考1"描述的最多,有严格的数学推导,但是不好理解,因为太数学化,没有很好的描述偏移error的概念,"参考2"较为简略,而且有点奇怪的用i+1/2这样的像素点位置,单独看估计看不懂,"参考3"的思路是从纯逻辑的思路来看的,没有数学推导,所以不太严谨,但是并没有较为完美的描述,于是,我找到了作者原来的论文,进行参考。才发现,"参考1"的推导比作者原来表述的还要详细,原论文以证明为主,但是同时要更加严谨一些,比如在"参考1"中直接提出了dUpper和dLower的概念,并以此为根据来判断像素点,事实上"参考6"是先提出了到直线的距离,然后根据(dLower-dUpper)与先前的点到直线的距离的差符号一致,才开始转入对dUpper和dLower的使用,同时,"参考6"也完整的描述了所有区段的算法使用。
另外,在查找资料的过程中,发现很多奇怪的现象,比如,为了简化Bresenham算法的推导,很多资料完全放弃了数学公式的推导,然后仅仅凭空的添加进0.5这个值,意思就是直线在k+1点过了下一个像素位置一半,那么就选择y+1点,不然就选择y点,如WIKI
,《The Bresenham Line-Drawing Algorithm
》,然后再煞有介事的提出进一步的优化方案,以消除这个浮点数。实际上,看过原论文以后,我发现这些资料简直就是误人子弟,因为在作者提出算法的时候就从来没有用过啥0.5这个值,而且作者在描述此算法的优点时,就明确的提到不需要浮点运算。也就是说,前面的那些误人子弟的推导,推导出来的东西,根本就不能称作Bresenham算法,但是偏偏广为流传。。。。。。。。。。。
因为该算法的推导较为复杂,而"参考1"已经写的很详细了,(加上原论文)我也懒得在此重新写一遍了。没有此书的人已经不必要再继续看了,这里在此补充一些"参考1"没有提到的信息,已经解决一些"参考1"的问题。
1.推导的严谨程度来说,直接的初始条件是从点yk及yk+1到直线距离,哪个近,选择哪个点,因为此距离差与文中提及的dLower和dUpper差一致,所以才可以转为判断pk。
2.所谓重新安排等式(莫名其妙),其实就是在式(3.13)右边乘以
,以形成Bresenham对决策参数的定义式。
3.你怎么样都不能在书中提及的条件下,将x0,y0,以及
带入式(3.14)计算得到
,这里还需要用到原作者论文中提到过的假设,那就是
,
,因为作者在之前有坐标系平移的一步,将新坐标系的原点移到(x0,y0)点,估计“参考1”的作者也不是完全理解算法,所以就马虎的忽悠一下企图过关了。
另外提醒大家,网络的资料有的时候还是谨慎着点看,还是较为权威的教材最靠谱,(虽然也不一定没有问题)学习算法时,第一次提出该算法的论文实在是最好的参考资料。因为"参考1"有上述我提到的3个问题,所以一开始我跟着学习总是很纳闷,结合了很多资料来看,又碰到一堆误人子弟的资料,还是原始资料最靠谱。。。。。。。别人可以理解这个算法,但是有人能够理解的比发明这个算法的人要透彻的吗?
参考:
1.计算机图形学, Computer Graphics with OpenGL, Third Edition, Donald Hearn, M.Pauline Baker著, 蔡世杰等译, 电子工业出版社
2.交互式计算机图形学--基于OpenGL的自顶向下方法(第五版),Interactive Computer Graphics -- A Top-Down Approach Using OpenGL, Fifth Edition 英文版 Edward Angel 著, 电子工业出版社
3.Windows游戏编程大师技巧(第二版), Tricks of the Windows Game Programming Gurus Second Edition, Andre Lamothe著, 沙鹰 译, 中国电力出版社
4.OpenGL 编程指南(第六版) OpenGL Programming Guide, OpenGL Archiecture Review Board, Dave Shreiner等著, 徐波 译, 机械工业出版社
6.Algorithm for computer control of a digital plotter
,J. E. Bresenham的关于Bresenham算法的原始论文,IBM Systems Journal 1965
原创文章作者保留版权 转载请注明原作者 并给出链接
write by 九天雁翎(JTianLing) -- www.jtianling.com
Posted By 九天雁翎 at 九天雁翎的博客 on 2010年10月25日